Abstract

The COVID-19 disease produced by the novel SARS-Cov-2 coronavirus has become a global pandemic that has affected, in one way or another, the socio-economic life of all humans. In order to analyze the morphology structure of it, the SARS-CoV-2 coronavirus samples are observed under the electron microscopic; and in [3,4], we proposed some algorithms to enhance the S-spikes in those microscopic images. In this work, we propose a new algorithm in order to overlap the obtained results of processing to original images, and we compared our algorithm with those proposed in MatLab.

Keywords: COVID-19; SARS-Cov-2; enhancement; segmentation; overlap.

Citation: Rodríguez R, Lau LD, Mboro GA, Mondeja BA, Raúl N Suárez ADY. SARS-Cov-2: A proposal of algorithm for the overlapping of high-resolution microscopic images. J Clin Images Med Case Rep. 2021; 2(5): 1376.

Introduction

One of the most significant characteristics of the novel SARSCov-2 coronavirus is its high contagion and rapid spread, and the severe acute respiratory syndrome broke out at the end of December 2019. From that date until now, more than 400 million people have been infected, and the death toll exceeds more than 4 million [1]. For this reason, the World Health Organization (WHO) has classified this pandemic (called COVID-19) as terrible.

For all the above, various scientific institutions, universities, large transnationals of the bio-pharmaceutical industry, among many others, have been in function of the study and characterization of this novel SARS-Cov-2 coronavirus.

It is known that Electron Microscopy (EM) is a widely used technique in the analysis of viruses and bacteria, which allows a rapid morphological identification of the infectious elements contained in a sample without the need for reagents and special considerations, and this technique is usually sufficient for the specialist to recognize an unknown infectious agent [2].

However, as was expressed in [3,4], microscopic images usually present some blurring problems, basically due to physical characteristics inherent to EM, such as: Out of focus, imperceptible vibrations, voltage changes, among other; which makes a correct analysis of them difficult.

In the case of the novel SARS-Cov-2 coronavirus, it is of great importance to improve the microscopic images of the S-Spikes because it allows a better visualization of these, which are associated with areas of greater virulence [3,4]. Sometimes, for later studies, it is important and necessary to be able to overlap the original microscopic images with those that one improved. The goal of this work is to propose a new algorithm that allows achieving efficiently the overlapping of two microscopic images. We compared the obtained results by using our strategy with those achieved using a MatLab function.

This work continues as follows: In Section II, we presented some related works. Section III describes our overlapping algorithm. Section IV presents the experimental results, and a discussion and analysis thereof. Finally, one can found the conclusions in Section V.

Related works

A common or standard method does not exist for overlapping of images. In general, every specialist applies his, often adapting it to the boundary conditions of images with which one has to work. However, there is a common factor in all the reviewed works and that require special consideration: the determination of real size of images, since it would be very difficult to compare scenes of different relative dimensions.

In the consulted literature, a publication appears where the authors transfer the images to the frequency space through the cosine discrete transform, there they perform the overlapping and then return to the coordinate space [5]. Although the results presented in the work are interesting, from a theoretical and practical point of view, moving from one space to another can generate losses. In another study [6], a refined algorithm for the union and mixing of images is exposed. In one of steps of the proposed strategy, one attenuates the effect of the overlapping through a cross-correlation method, which is used in order to determine and select the best point between any new image and the previous composite one. In addition, they use a complementary technique to mix images, which is based on a gradient method that eliminates abrupt changes in intensities at the union of scenes. The disadvantage of this technique is that it can slow down if one takes a very large window to perform the correlation.

In another work that appears in [7], they offered an algorithm for the joining of images, which it uses the characteristics of the scenes seen from unmanned aerial vehicles. The purpose of this strategy is the detection and grouping of qualified images for their combination or mixture, carrying out this process from the determination of key points. However, the selection of these key points is not trivial, and can become a weak step of the algorithm.

In [8], the authors presented a strategy for the alignment of several images, where the principle consists on overlapping the common characteristics of the same ones. The technique employs a transfer strategy, and finds the required displacement vectors through a cross-correlation using a fast Fourier transform. Here too, the disadvantage of this algorithm is the transfer to another space, which can bring its complications.

Our algorithm proposal

As we expressed, the main goal of this work is to achieve, in a simple way, the overlapping of two microscopic images.

We need to fuse to the original images the result of the improved microscopic images of the novel SARS-Cov-2 coronavirus, where one can achieve a match, as accurate as possible, of the enhanced S-Spikes. This will allow the specialist to have a more harmonious panoramic view of the processing effect, and at the same time, a more realistic idea of density and spatial distribution of the S-Spikes.

In the previous section was noted that the proposed strategies, besides that they are not designed for the fusion of micro-images, present certain algorithmic complexities, and some work in other spaces. This was what motivated us to develop the algorithm detailed below.

Overlapping algorithm between micro-images

Data: Let B1 and B2 be the micro-images to be overlapped;

Result: Let C be the image resulting from the overlapping;

1. Calculate the size of image B1 (number of rows and columns), let N, M be;
2. Calculate the size of image B2 (number of rows and columns), let N1, M1 be;
3. Calculate between the two images the highest value of the rows and columns, let Nmax (max (N, N1)) and Mmax(max (M, M1)) be
4. Obtain the center of mass of the maximum row and column, let CNmax (fix (Nmax / 2)) and CMmax (fix (Mmax/ 2)) be;
5. Creation of two temporary matrices, let TempB1 ((Nmax, Mmax) = 0) and TempB2 ((Nmax, Mmax) = 0) be;
6. Obtain the center of mass of image B1, let CnB1 (fix (N / 2)) and CmB1 (fix (M / 2)) be; 7. Calculate the difference between the centers of mass, let DifCn (fix (CNmax-CnB1)) and DifCm (fix (CMmax-CmB1)) be;
8. Deposit the image B1 in the temporary matrix TempB1 taking as reference the difference of the centers of mass calculated in the previous step, that is; for y = 1, N for x = 1, M TempB1(DifCn+y, DifCm+x)= B1(y, x);
9. Obtain the center of mass of image B2, let CnB2 (fix (N1 / 2)) and CmB2 (fix (M1 / 2)) be;
10. Calculate the difference between the centers of mass, let DifCn1 (fix (CNmax-CnB2)) and DifCm1 (fix (CMmaxCmB2)) be;
11. Deposit the image B2 in the temporary matrix TempB2 taking as reference the difference of the centers of mass calculated in the previous step, that is; for y = 1, N1; for x = 1, M1; TempB2(DifCn1+y, DifCm1+x)= B2(y, x);
12. Return to matrix C an image of the same size as TempB1 and TempB2, and with the elements of maximum values, let C = max (TempB1, TempB2) be the result of the overlapping;
13. Return C;

One can observe that the proposed overlapping algorithm does not need to pass to another space; it works directly on the spatial coordinates of input images. Here, the important issue is the determination of the centers of mass in order to achieve the exact coincidence of the improved S-Spikes in relation to those of original image. It is known that, generally, when one carries out some kind of contrast enhancement, the size of processed image changes relative to original, especially when the procedure involves convolution. Today, many of efficient algorithms for image enhancement are carried out through local operations (generally through convolutions); thus, one takes into consideration the correlation between pixels, and the obtained results are a lot of better [9].

The performance of this algorithm was tested in a database of more than 1000 microscopic images of the novel SARS- Cov-2 coronavirus [2,3], and the obtained results were compared with those achieved by using a MatLab function.

Results analysis and discussion

The used microscopic images in these experiments were taken from nasopharyngeal samples from COVID-19 positive patients. In Figure 1, we show some examples of typical images of the novel coronavirus, where one can observe the blurring characteristic of the S-Spikes (hyper-dense white areas).

One can observe in Figure 1 that the S-Spikes are small points lighter than the background around them, grouped in hyperdense areas corresponding to the virus and scattered throughout the image. Important to note that the S-Spikes do not follow a particular pattern, but spatially have a random distribution [2]. In addition, by the physics of formation of these microscopic images, one can appreciate as a fundamental characteristic, a certain tendency to a level of blurriness, which persists even in high-resolution microscopes.

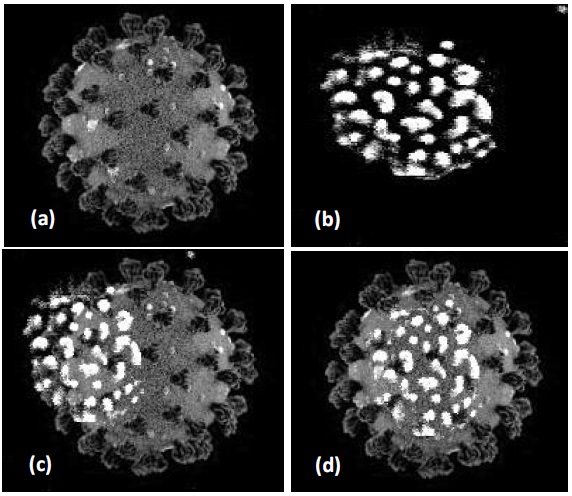
In Figure 2, we present other examples of microscopic images of the novel SARS-COV-2 coronavirus, taken from positive patients with COVID-19. One can see that a certain degree of blurring of the S-spikes persists (white points). For the specialists, and given the research that were being carried out, it was necessary to improve the contrast of the S-Spikes (and in some cases isolate these proteins) [2,3], and later, to overlap the result of enhancement with the original microscopic images.

We found that some of the published strategies (see Section II) were developed for other purposes, and they had algorithmic complexity. For this reason, we developed the algorithm presented in Section III. One can see that our strategy is simple and easy to implement.

Next, we will expose the results obtained in the improvement of the S-Spikes by applying one of the algorithms published in [2], and the overlapping carried out using a MatLab function. We verified that sometimes this function was wrong and did not achieve a correct overlap in the microscopic images. One can see that there is a slight displacement between them; that is, a shift of the improved image in relation to its original. This may happen because of the alteration in size (decrease) that occurs in the processed image, when using a convolution technique.

In Figures 3, 4, 5 and 6, we show the obtained results in the improvement of S-spikes. One can observe the overlays carried out with the enhanced images and the originals by using a MatLab function and our algorithm. We used, for comparison, a MatLab function because we did not find a strategy that would fit the goal of this work, which one could appreciate in Section II.

By observing the result of overlapping, one can verify that, in fact, the MatLab function is wrong three times, while our strategy evidences better performance. For this application, the specialists needed to have a satisfactory match of the improved S-Spikes in relation to their originals, in order to obtain a more accurate panoramic view of the surface density of the S-Proteins, which is closely related to the degree of virulence of the novel SARS-Cov-2 coronavirus [2,3]. The higher the surface density index of S-proteins, the higher the degree of virus activity in that area.

The goal of comparing our algorithm with another strategy, and in particular, with a MatLab function, was in order to determine the effectiveness of our proposal. However, we continue working on further improving the accuracy of our algorithm. Indeed, one can see in the image of Figure 4 (d) a very slight shift when using our strategy, which may be related to the rounding we carried out in obtaining the centers of mass from the microscopic images.

We verified that in a run of 104 overlapping carried out, our algorithm showed an efficiency of 98.9 %, while the effectiveness of the MatLab function was 35.7%. We observe that when the images to be overlapped have very similar dimensions, the MatLab function is not wrong. Our algorithm showed more stable performance on images of different dimensions.

In Figures 7, 8, 9 and 10, we present other examples of overlapping carried out with our algorithm. We also show the obtained results by using the MatLab function

Conclusion

In this paper, we proposed an algorithm with the goal of achieving a better accuracy in the overlapping of two microscopic images. In this particular case, among the improved and original images of the novel SARS-Cov-2 coronavirus. We verified the obtained good results with our strategy in the overlapping of the S-Spikes, and not so when we used a MatLab function. The use of this algorithm can be easily extended to other bio-image overlapping applications.

References

1. https://news.google.com/covid19/map?hl=es-19&mid=%2Fm %2F02j71&gl=CU&ceid=CU%3Aes-419
2. Rodríguez R, Mondeja BA, Lau LD, Vizcaino A, Acosta EF, et al. The SARS-Cov-2 Novel Coronavirus: A Reflection about Enhancement of High- Resolution Microscopic Images. J Bacteriol Parasitol. S10: 004. 2021.
3. Rodríguez R, Mondeja BA, Valdés O, Resik S, Vizcaino A, et al. SARS-CoV-2: enhancement and segmentation of high- resolution microscopy images-Part I”. Signal Image Video Process. 2021; 23: 1-9.
4. Rodríguez R, Mondeja BA, Valdés O, Resik S, Vizcaino A, et al. SARS-CoV-2: Theoretical analysis of the proposed algorithms to the enhancement and segmentation of high-resolution microscopy images- Part II. Signal Image Video Process, accepted, 2021.
5. M. Shahid Farid, Arif Mahmood. An Image Composition Algorithm for Handling Global Visual Effects”. Multimedia Tools and Applications. 2014; 71: 699-1716.
6. Rankov V, Locke RJ, Edens RJ, Barber PR, et al. An algorithm for image stitching and blending. Proceedings of SPIE -- Volume 5701: Three-Dimensional and Multidimensional Microscopy: Image Acquisition and Processing XII, Jose-Angel Conchello, Carol J. Cogswell, Tony Wilson, Editors. 2005
7. M. Phil B, Marcos N. Feature-Based Stitching Algorithm of Multiple Overlapping Images from Unmanned Aerial Vehicle System. Asian Journal of Business and Technology. 2018; 1: 2.
8. Swoger J, Verveer P, Greger K, Huisken J, E. H.K. Stelzer. Multiview image fusion improves resolution in three-dimensional microscopy”, J. Opt. Soc. Am. 2007; 15.
9. Rodríguez R, Garcés Y, Torres E, Sossa H, Tovar R. A vision from a physical point of view and the information theory on the image segmentation”, Journal of Intelligent & Fuzzy Systems. 2019; 37: 2835-2845.