Abstract

Scoliosis is a disease caused by the abnormal curvature of spine. Generally, curvature above 10 degrees is considered as a scoliosis. About 2-4% of the world population is affected by this disease. Therefore, there is a need for such a tool that can help surgeons and bioengineers to study the behavior of a spine under various conditions. Considering the engineering perspectives, it is necessary to understand the fundamental anatomy of the human spine and pathological techniques associated with the orthopedic conditions, so that better technologies can be implemented. The main objective of this work is to develop a 3D model that can simulate various orthopedic conditions associated with the change in Cobb angle. CT scans of patients are obtained from the Spine center of G. hospital, Lahore. 3D Models of actual patients are created using 3D Slicer and Radiant software. Only spine portions are extracted to understand the type of scoliosis, curvature region, and Cobb angles. The cobb angle of each of the patients is measured using Solid Works software. Considering the real data of patients, the severity level of scoliosis in the patients is discussed.

Keywords: anthropometry; Cobb angles; CT scans; scoliosis; Spine deformity; vertebra.

Citation: Ali A, Baqir MF, Kashif A, Nawaz MH, Shahid MK. 3D modeling of human spine and the cobb angle measurement in scoliosis patients. J Clin Images Med Case Rep. 2021; 2(6): 1495.

Introduction

In the human spine, 23 small bones called vertebra are located in horizontal sequence to make the spinal column [1]. Each vertebra is named with the help of numbers and letters. The letters indicate the regions such as C for cervical, T for thoracic, and L for lumbar, and the number indicates the positions of a vertebra in the specific area. Human spine is divided into four regions [2]. The first region is the cervical vertebra located in the neck and is seven in number [3] represented as C1-C7. C1 and C2 have distinct characteristics for special moments [4]. C1 vertebra is known as atlas whereas, C2 vertebra is named as axis and is next to C1. C6 and C7 vertebrae are of greater size than that of other cervical vertebrae, as they are in transition to the thoracic region. The second region is named as a thoracic vertebra consists of 12 vertebrae (T1–T12) associated to the chest zone. Thoracic vertebra helps to link two ribs with each other and limits their movement [5]. Third region is the lumbar region consists of five lumbar vertebrae (L1–L5). The first and upper area is categorized by a reduction in the depth of the spinal cord from L1–L3 [6]. The second region is the central lumbar region and is known by a narrow spinal canal and L3 vertebra. The third and lower area is a transition from lumbar to sacral. The last region is the Sacrococcygeal that has nine fused vertebrae. The sacrum is lower to the lumbar region and has a bony structure like a shield. It is linked to sacroiliac joints in the pelvis.

Generally, the side view of an adult spine reveals the Sshaped curvature. The cervical and lumbar regions consist of a concaved shape curve whereas, the convex shaped curves are displayed by thoracic and sacral regions. The combined framework of these two arcs works like a spring having a coiled shape as a shock absorber and permit define motion through the spinal column [7]. Hence, the first, second and third curves are known as the cervical, thoracic and lumbar curve, respectively [8]. Several methods are known for the analysis of vertebra in human spine. Radiography is a foremost technique for the examination of the body organs like joints, injured bones, and spines [9] and is helpful to examine the morphological characteristics of body part or organs for diagnosis purposes of orthopedics [10]. The magnetic resonance imaging [11] uses the radio waves, strong magnetic fields and magnetic field gradients to generate images of the spine with clear visualization [12]. A Computerized Tomography scan (CT scan) is the combination of computers and rotating X-ray machines to generate the crosssectional images of the body parts such as bones, soft tissues, blood vessels, etc. [13,14].

Scoliosis is a term referred to any unnatural ebb and flow, anomalous or sideways arch of the spine [15]. It is the one of common diseases associated with the musculoskeletal system and also referred as the 3D abnormality of the spinal curve [16]. It may contain a single curve like letter C or can have two curves like letter S and it grows with the time if develop in the patients [17]. Scoliosis can occur in the lumbar region and the thoracic region. Sometimes this curvature belongs to both regions and is known as the thoracic-lumbar region. It is observed that scoliosis affects three out of a hundred patients that may results in abnormal lifestyle of patient, if not treated in time[18]. Scoliosis is an essential angle in inspecting the side effects and analytic strategy of the spine as it helps in characterizing the parameterization of the basic elements in models [19]. Scoliosis is categorized based on the shape, location, direction, and severity of the curvature.

Computer-generated models are of great importance in the field of biomedical to do better analysis and predict the behaviors under different conditions. Many models are developed in different CAD software to study the behavior and dynamics of the spine [20]. However, the specificity of spine model is of great importance because of the variable scoliotic conditions among the patients. As several software and different techniques for medical imaging are available these days, it is possible to develop parametric models of the human spine. Such models allow us to find human spine curvatures in terms of Cobb angle adjustments [21]. The main objective of this study is to offer a model that will assist to surgeons in identifying the finest treatment methods for remedial surgery. The parametric model of the human spine would be a tool to stimulate spine curvatures having scoliosis and allow cob angles adjustments.

Methodology and modeling

Anthropometric data

Anthropometry is the term used for the measurement of all physically described features or characteristics related to the human spine. These obtained measurements are used to design an efficient model. This technique has been applied in the study of ergonomics during modeling [23]. A study provided the quantitative 3D data of the anatomy related to the human spine [24]. This data provides information about the angular relations and linear dimensions of different regions of the small bony structure [25]. Linear regression, standard deviation, and mean were considered in data collection.

CT Scans and visualization

The data of the scoliosis patients is obtained from The Spine Center of G. Hospital, Lahore, Pakistan. The patients of different age group suffering with different type of scoliosis were considered for data collection. The models were generated for each of the patients and further processing was done as per defined parameters. CT scan data is visualized by Radiant software, a userfriendly software for the visualization of CT scans [26]. The 3D image of the patient is generated that can be rotate and scroll.

Modeling using radiant

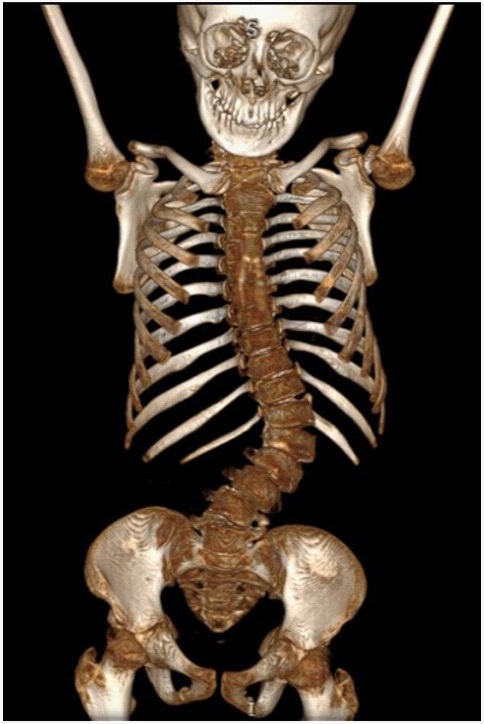
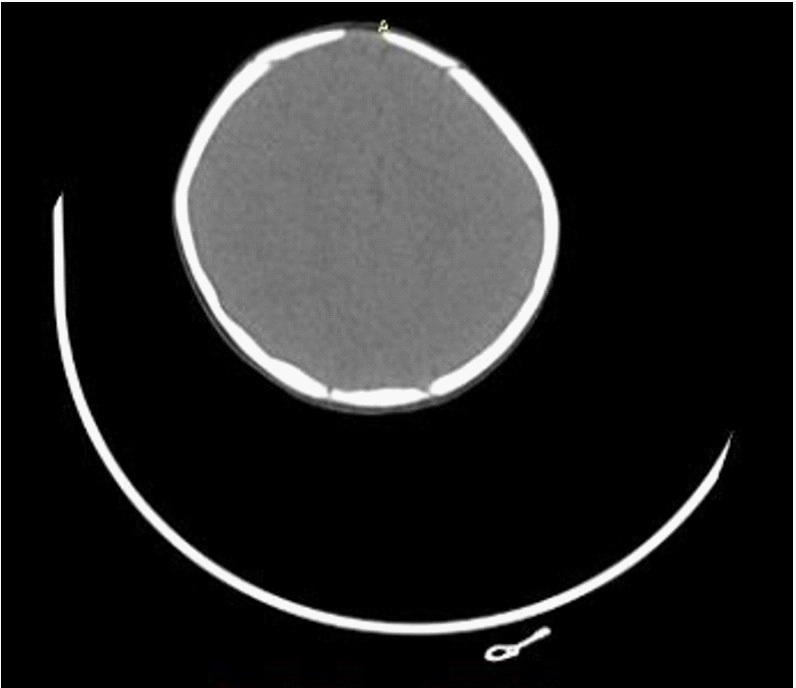
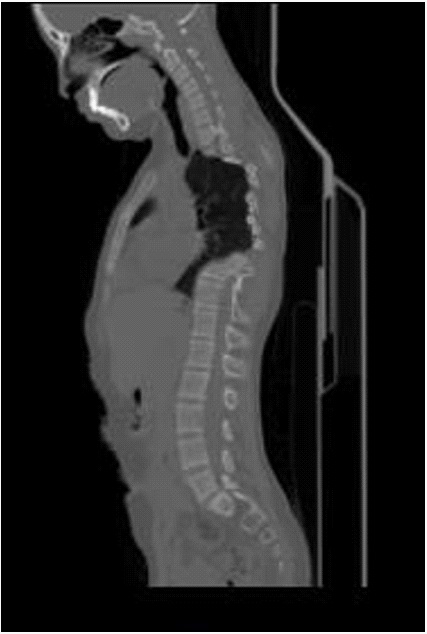
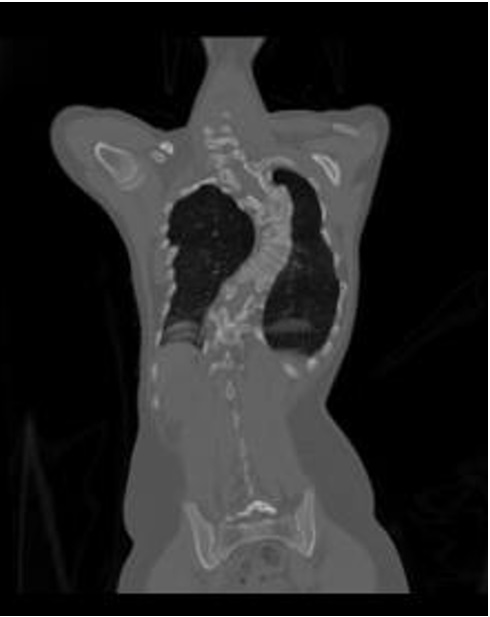
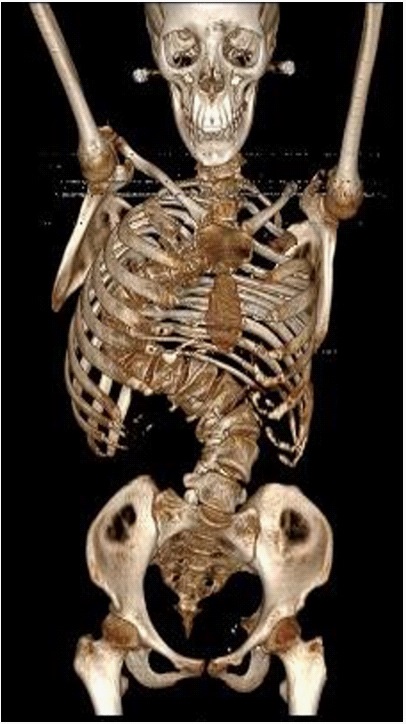
Radiant is a software designed for the analysis of medical images such as CT scans. It can convert a simple CT scan into a 3D model [27]. 3D Volume Rendering (VR) assists to convert it into a comprehensive 3D model. Once the DICOM file opens in Radiant, an axial, 3D, and sagittal views can be seen (Figure 1-4).

The 3D VR tool allows the visualization of large volumes of data generated by modern CT/MR scanners in 3D space. Different aspects of the data set can be interactively explored in the 3D VR window.

This tool allows to rotate the volume, change zoom level and position, adjust color and opacity, measure the length, and show hidden structures by cutting off the unwanted parts of the volume using scalpel tool. The image is rendered progressively to maintain fluid operations even on slower machines. In this study, spine structure is cropped for further analysis (Figure 5-6).

Cobb angle measurements

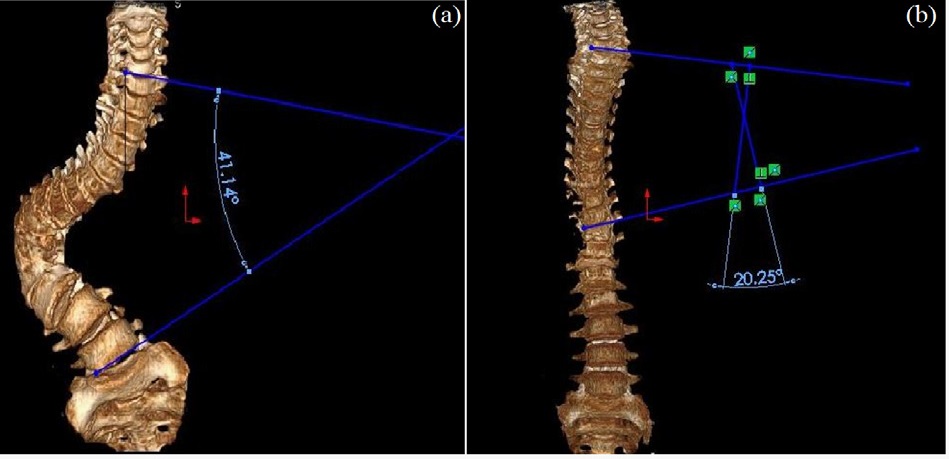
Cobb angle is defined as the angle between the two vertebrae that starts from the region where deflection starts and ends at the end point of deflection. The 3D model of each of the patients is obtained and their cobb angles are calculated. Generally, two methods are known for determining the cobb angle that are direct and geometrical methods [28].

In direct method, a horizontal line is drawn from the vertebrae where the deflection starts, and another line is drawn from the vertebrae where the deflection ends. Then, these two lines are extended, and where these lines intersect, the calculated angle is termed as cobb angle (Figure 7a). The geometrical method is used when the lines can intersect with each other once they are extended. In this case, a perpendicular is extended from each of the lines. The cobb angle is determined at the point where the perpendicular intersects (Figure 7b).

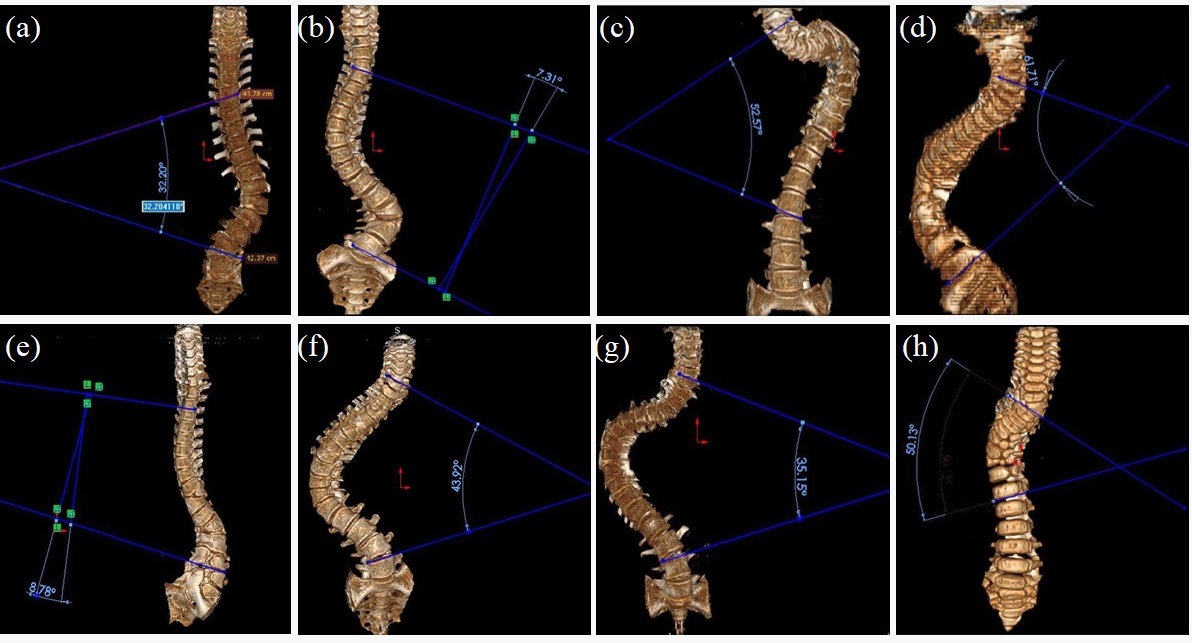
Cobb angle of each of the patient is calculated and their regions are also determined. Some of the patient’s cobb angles are manifested in Figure 8. The cobb angles of the patients were calculated using both direct and geometrical methods. The direct method is applied to measure the cobb angle of spines in Figure 8a, c, d, f, g, and h having values of 32.20°, 52.57°, 61.71°, 43.92°, 35.15° and 50.13°, respectively. For Figure 8b and e, the only potential way to calculate the cobb angle is the geometric method, because the extended lines do not intersect each other. So, we extended the normal on each line and measured the angle which is found to be 7.31° and 8.78° for spine in subfigure b and e respectively

Results and discussion

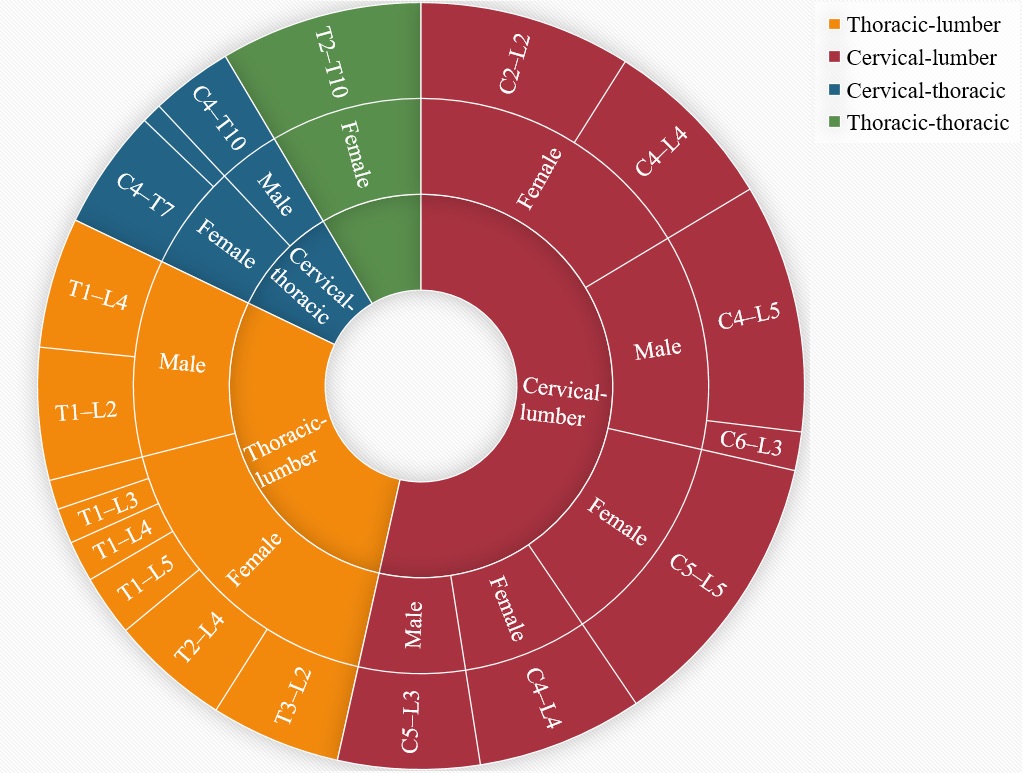
The data obtained from the scoliosis patients is presented in Table 1. The higher number of patients were found to have deflection in thoracic-lumber and cervical-lumber regions. About 8 patients were observed with abnormal cobb angle in thoraciclumbar region. Only three patients were noticed to have deflection in cervical-thoracic region. The sacral and coccyx are the fixed regions, therefore, they do not contribute in scoliosis [29]. Based on the degree of curvature, the risk-level of scoliosis can be determined.

Table 1:Description of data obtained from the patients.

The low-risk scoliosis is considered when the patients have 10-19°curvature. Generally, patients in this category remains in safe state and cannot be operated. At this level, scoliosis can be controlled with specific exercises and regular medical examination. It has been estimated that 2-3% population of the world affected by this and the reason for this is not well established. This type of scoliosis is called idiopathic scoliosis [30]. One of the reasons behind this is the unequal growth of the spine and spinal cord that causes stress in the structure resulting in the scoliosis [31]. The common symptoms include variation in each side of hip, shoulder and legs or the displacement of rib-cage.

The moderate-risk scoliosis is referred to the curvature in range of 20-40° degrees and can be treated through proper medication and bracing. About 0.3% population is estimated to suffer with moderate-risk scoliosis. Bracing helps to mitigate an increase in the curvature of the spine and to evade surgery [32]. If this does not serve the purpose, then the doctor will advise the surgery, which can straighten the spine and control the further increase in the curvature. Scoliosis above 40° is considered as a severe-risk scoliosis and it is found in about 0.1% population. It usually occurs in the thoracic-lumbar region. In this condition, the doctor recommends surgery, and the maximum possible straightening of the spine is done. Figure 9 exhibits the higher risk of scoliosis in females as compared with male patients that is found in fine agreement with reported studies [33].

This study emphasized the 3D modeling of the human spine to examine the scoliosis progression in the patients. The visualization of CT scan data and the model development using Radiant software enables the analysis of curvature in different regions of spine that further helps to calculate cobb angle. The application of model for a new patient will needs the paramedical staff to upload upright full spine x-ray and standard medical data in the system for comparison and further determination of cobb angle. Considering the physical attributes of patients such as age and age, the 3D modeling and cobb data analysis can help to predict the severity of cobb angle in future or at maturity level [34]. Hence, this technique is strongly associated with the decisions lead to the medication, bracing, or surgery of the patients.

Conclusion

This study details the model that will assist to surgeons in classifying the finest treatment methods for remedial surgery. The parametric model would be helpful to stimulate spine curvatures having scoliosis. The cobb angle adjustment will enhance the practicality of the technique. It is found that the actual deflection deviates from the model because many other parameters affect the curvature of the patients. The cobb angle was remarkable increased by increasing displacement above 50 mm. The higher deflection is observed in thoracic-lumber and cervical-lumber regions. The higher deflection is observed in the thoracic-lumbar region because of the higher displacement in this section. The model showed maximum value of cobb angle (70.43°) for the section C5-L5 in cervical-lumber region. Cobb angle is greatly affected by the value of the epical displacement, as more the epical displacement more will be the cobb angle and more the value of deflection

Declarations

Declaration of competing interest: We certify that there is no conflict of interest with any financial organization regarding the material discussed in the manuscript.

Funding: This research did not receive research grant from any funding agency in the public, commercial, or not-for-profit sectors.

References

1. Devereaux MW. Anatomy and Examination of the Spine. Neurologic Clinics. 2007; 25: 331–351.
2. Crawford RP, Cann CE, Keaveny TM. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone. 2003; 33: 744–750.
3. Alizadeh M, Knapik GG, Mageswaran P, Mendel E, Bourekas E, Marras WS, et al. Biomechanical musculoskeletal models of the cervical spine: A systematic literature review. Clinical Biomechanics. 2020; 71: 115–124.
4. Nuckley DJ, Linders DR, Ching RP. Developmental biomechanics of the human cervical spine. Journal of Biomechanics. 2013; 46: 1147–1154.
5. Suarez-Escobar M, Rendon-Velez E. A survey on static and quasistatic finite element models of the human cervical spine. International Journal on Interactive Design and Manufacturing. 2018; 12: 741–765.
6. Weber CI, Hwang CT, van Dillen LR, Tang SY. Effects of standing on lumbar spine alignment and intervertebral disc geometry in young, healthy individuals determined by positional magnetic resonance imaging. Clinical Biomechanics. 2019; 65: 128–134.
7. Dascalescu VI. Parametric model of a human spine to model scoliosis. 2016.
8. Kingma I, Busscher I, van der Veen AJ et al. Coupled motions in human and porcine thoracic and lumbar spines. Journal of Biomechanics. 2018; 70: 51–58.
9. Pinheiro AP, Coelho JC, Veiga ACP, Vrtovec T. A computerized method for evaluating scoliotic deformities using elliptical pattern recognition in X-ray spine images. Computer Methods and Programs in Biomedicine. 2018; 161: 85–92.
10. Chung N, Cheng YH, Po HL et al. Spinal phantom comparability study of Cobb angle measurement of scoliosis using digital radiographic imaging. Journal of Orthopaedic Translation. 2018; 15: 81–90.
11. He L, Liu Z, Liu C et al. Radiomics Based on Lumbar Spine Magnetic Resonance Imaging to Detect Osteoporosis. Academic Radiology. 2020: 1–7.
12. Berry DB, Hernandez A, Onodera K, Ingram N, Ward SR, Gombatto SP, et al. Lumbar spine angles and intervertebral disc characteristics with end-range positions in three planes of motion in healthy people using upright MRI. Journal of Biomechanics. 2019; 89: 95–104.
13. Girdler S, Cho B, Mikhail CM, Cheung ZB, Maza N, Kang-Wook Cho S. Emerging Techniques in Diagnostic Imaging for Idiopathic Scoliosis in Children and Adolescents: A Review of the Literature. World Neurosurgery. 2020; 136: 128–135.
14. Mishra P, Singh SK, Ranjan V, Singh S, Pandey A, Sharma H, et al. Measurement of spine parameters and possible scoliosis cases with surface topography Techniques: A case study with young Indian males. Measurement: Journal of the International Measurement Confederation. 2020; 161: 107872.
15. Rustenburg CME, Kingma I, Holewijn RM et al. Biomechanical properties in motion of lumbar spines with degenerative scoliosis. Journal of Biomechanic. 2020; 102: 109495.
16. Kelly A, Younus A, Lekgwara P. Adult degenerative scoliosis-A literature review. Interdisciplinary Neurosurgery: Advanced Techniques and Case Management. 2020; 20: 100661.
17. Liu Y, Pan A, Hai Y, Li W, Yin L, Guo R. Asymmetric biomechanical characteristics of the paravertebral muscle in adolescent idiopathic scoliosis. Clinical Biomechanics. 2019; 65: 81–86.
18. Compton J, Voort W Vander, Weinstein S. Scoliosis Curvature Follows Thoracic Organ Orientation. Spine . 2020; 45: 378–380.
19. Bourdon E, Graham RB, van Diëen J. A comparison of methods to quantify control of the spine. Journal of Biomechanics. 2019; 96: 109344.
20. Pouya S, Khodabakhsh M, Spröwitz A, Ijspeert A. Spinal joint compliance and actuation in a simulated bounding quadruped robot. Autonomous Robots. 2017; 41: 437–452.
21. Jalalian A, Gibson I, Tay EH. Computational biomechanical modeling of scoliotic spine: Challenges and opportunities. Spine Deformity. 2013; 1: 401–411.
22. Harty JA, Quinlan JF, Kennedy JG, Walsh M, O’Byrne JM, et al. Anthropometrical analysis of cervical spine injuries. Injury. 2004; 35: 249–252.
23. Sagot JC, Gouin V, Gomes S. Ergonomics in product design: Safety factor. Safety Science. 2003; 41: 137–154.
24. Panjabi MM, Takata K, Goel V et al. Thoracic human vertebrae quantitative three-dimensional anatomy. Spine. 1991.
25. Choong CL, Alias A, Abas R et al. Application of anthropometric measurements analysis for stature in human vertebral column: A systematic review. Forensic Imaging. 2020; 20: 200360.
26. Alrehily F, Hogg P, Twiste M, Johansen S, Tootell A. The accuracy of Cobb angle measurement on CT scan projection radiograph images. Radiography. 2020; 26: e73–e77.
27. Shen K, Clement RC, Yaszay B, Bastrom T, Upasani V V, Newton PO, et al. Three dimensional analysis of the sagittal profile in surgically treated Lenke 5 curves in adolescent idiopathic scoliosis. Spine Deformit. 2020; 28.
28. Campbell-Kyureghyan N, Jorgensen M, Burr D, Marras W. The prediction of lumbar spine geometry: Method development and validation. Clinical Biomechanics. 2005; 20: 455–464.
29. Yamato Y, Sato Y, Togawa D et al. Differences in the geometrical spinal shape in the sagittal plane according to age and magnitude of pelvic incidence in healthy elderly individuals. Journal of Orthopaedic Science 2019: 1–8.
30. Ogilvie JW. What’s Important: Moving Beyond “Idiopathic” in Adolescent Idiopathic Scoliosis. The JOURNAL OF BONE AND JOINT SURGERY. 2020; 102: 269–270.
31. Uehara M, Takahashi J, Ikegami S, et al. Determination of optimal screw number based on correction angle for main thoracic curve in adolescent idiopathic scoliosis. Journal of Orthopaedic Science. 2019; 24: 415–419.
32. Antoine L, Nathan D, Laure M, Briac C, Jean-François M, Corinne B. Compliance with night-time overcorrection bracing in adolescent idiopathic scoliosis: Result from a cohort follow-up. Medical Engineering and Physics. 2020; 77: 137–141.
33. Pettersson K, Wagner P, Rodby-Bousquet E. Development of a risk score for scoliosis in children with cerebral palsy. Acta Orthopaedica. 2020; 91: 203–208.
34. Nault ML, Beauséjour M, Roy-Beaudry M et al. A Predictive Model of Progression for Adolescent Idiopathic Scoliosis Based on 3D Spine Parameters at First Visit. Spine. 2020; 45: 605–611.